Você deve ter estudado os tópicos "Aritmética Básica" e "Exponenciais" antes de começar por aqui.
Este tópico vem após exponenciais pois é usado como a "volta" da exponencial. Veja só:
Sabemos que 5 elevado à potência 2, resulta 25, agora mudamos o contexto e vou fazer uma pergunta:
- Qual o número (expoente) que devemos elevar o 5 para obtermos 25?
Você deve estar pensando:
-Mas isso eu resolvo com exponenciais!!!
Sim, porque essa é bem fácil, as difíceis não saem tão simples assim. Vamos começar de baixo.
O logaritmo serve para isso!
Esta pergunta poderia ser interpretada matematicamente da seguinte forma:
Como sabemos que devemos elevar o 5 ao quadrado (ou seja, à potência 2) para obtermos 25, chegamos à conclusão que o logaritmo de 25 na base 5 é 2:
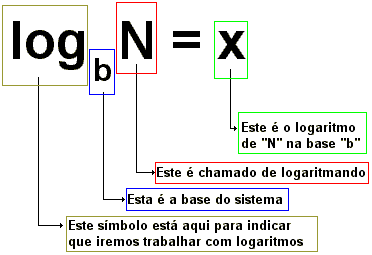
Note que, anteriormente, dissemos que "x" é o expoente de "b", e na figura acima está escrito que "x" é o "logaritmo". Isso acontece pois o LOGARITMO É UM EXPOENTE.
Agora, com esta breve introdução, podemos escrever uma primeira definção de logaritmo (hei, ainda não é a oficial, mas é o que temos até agora):
| Logaritmo de um número N, na base b, é o número x ao qual devemos elevar a base b para obtermos N. |
Esta é a apenas uma definição, você deve ter entendido bem o que está escrito acima dela para ir ao próximo capítulo de estudo.
Veremos quais as condições que a base, o logaritmando e o logaritmo devem satisfazer para termos um logaritmo.
Nenhum comentário:
Postar um comentário